
Statistical process control provides this context for understanding histograms.įigure F.17 Two Histograms: (A) Histogram of symmetric Since the histogram does not consider the sequence of So the histogram that looks like it fits our needs could have come from data showing random variationĪbout the average or from data that is clearly trending toward an undesirable condition. A histogram with a given shape may be produced by many different processes, the onlyĭifference in the data being their order. One problem that novice practitioners tend to overlook is
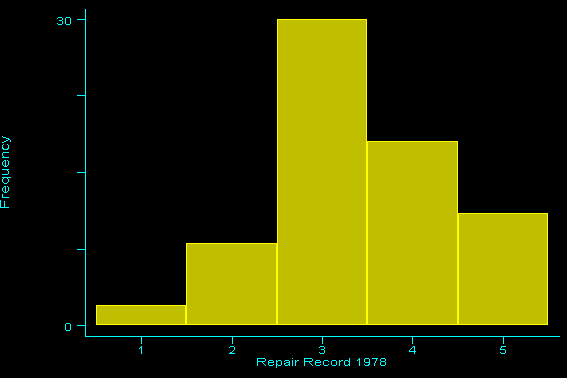
Implies a greater risk of error for interpreting histograms. Realistic view of a process distribution, although it is not uncommon to use a histogram when you have Over a larger sample period may be much wider, even when the process is in control. The histogram provides a view of the process as measured. Determining this can make understanding histograms easier. If double or multiple peaks occur, look for the possibilityĬoming from multiple sources, such as different suppliers or machine adjustments. Is a sharp demarcation at the zero point representing a bound. The majority of the data is just above zero, so there Skewed distribution, and may also be bounded, such as the concentricity data in Figure F.17B.Ĭoncentricity has a natural lower bound at zero, since no If it appears skewed, you should understand the cause of this behavior. If the data isĪbout the center of the histogram, it is skewed. If your data is from a symmetrical distribution, such asīell-shaped normal distribution as shown in Figure F.17A, the data will be evenly distributed about the center of the data. We can also see if the data is bounded or if it has symmetry, such as is evidenced The variation is also clearly distinguishable: weīetween 75.003 and 75.007. In Figure F.16, the central tendency of the data is about 75.005. Therefore, always use a control chartĭetermine statistical control before attempting to fit a distribution (or interpret the histogram).Īn excerpt from Six Sigma DeMYSTiFieD (2011 McGraw-Hill) by Paul KellerĪn advantage of the histogram is that the process location Out of control, then by definition a singleĭistribution cannot be fit to the data. If double or multiple peaks occur, look for the possibility that the data isĬoming from two different sources, such as two separate personnel groups, or two differently adjusted machines. The lower bound may be physically limited to zero.
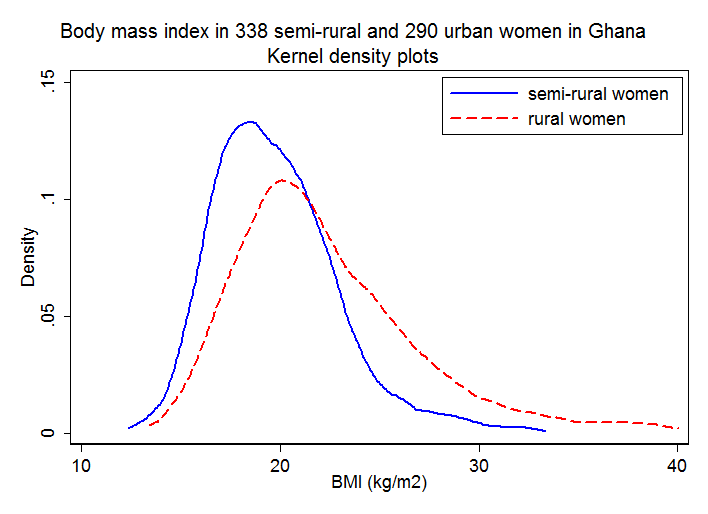
Some processes will naturally have a skewed distribution, and may also be bounded. Should understand the cause of the "skewness". If the data is not roughly evenly distributed about the center of the histogram, it is commonly called "skewed". If your data is from a symmetrical distribution, such as the Normal Distribution, the data will be evenly distributed about theĬenter of the data. This uses the undocumented command twoway_histogram_gen ( ).Interpretation is the resulting shape of a distribution curve superimposed on the bars to cross most of * Match sampling weights to k = 2 decimal places:Į.g. webuse nhanes2b, clearĪgrees with original weight to any degree of accuracy */ It turns out that all the weights are integers, so the conversion trick isn't needed. In this example, I use the nhanes2b data set.

The other functions are means, so are invariant to multiplication of the original weights. The only option unavailable will be the frequency option of histogram. (The trick is due to Austin Nichols.) This will permit you do use the above commands. However you can create frequency weights that will be multiples of the probability weights and agree in precision to any desired accuracy. The problem with sampling weights is that they can be non-integral. The histogram, kdensity, and cumul commands all take frequency weights, which must be integers.


 0 kommentar(er)
0 kommentar(er)
